
Summer School
About
The summer school covers new developments in arithmetic and p-adic geometry. In particular, the summer school touches topics in algebraic number theory, condensed mathematics, p-adic dynamics and Higher Hida and Coleman theory. It consists of four courses, accompanied by poster sessions presented by participants.
Speakers
Mini-Courses

Condensed Mathematics
Juan Esteban Rodriguez
In this minicourse we will review the foundations of condensed mathematics and give a first look to Analytic Geometry motivated from classical problems. (back)
More
Condensed mathematics is a new area created by Clausen and Scholze that conciliates the long standing problem of doing "topological algebra" in a categorical way. One of the most fruitful and novel theories developed in the realm of condensed mathematics is Analytic Geometry, a whole new extension of algebraic geometry that includes classical analytic geometry theories such as complex analytic geometry, differential geometry, rigid/adic/Berkovich geometry, etc. Some of the first outstanding applications of the theory is the definition of a well behaved theory of quasi-coherent sheaves for complex/adic spaces, the development of new cohomology theories in p-adic analytic geometries, and the geometrization of the real local Langlands correspondence by Scholze.
References
Higher Hida and Coleman theories and their connection to p-adic
L-functions
Andrew Graham, Giada Grossi
In this course, we will introduce higher Hida/Coleman theory for various examples of Shimura varieties, and discuss recent applications of this theory to the construction of p-adic L-functions. (back)
More
Higher Hida/Coleman theory concerns the study of p-adic/overconvergent automorphic forms in higher degrees of coherent cohomology of Shimura varieties, and is a particularly important tool for understanding the arithmetic of p-adic Galois representations and their associated L-functions.

Hecke orbits and equidistribution
Sebastián Herrero
In this minicourse we will
study Hecke orbits on modular curves and their equidistribution properties. (back)
We will start by recalling the definition and arithmetic properties of
Hecke orbits in relation to isomorphism classes of elliptic curves over
algebraically closed fields and isogenies between them.
Then, we will explain the work of Clozel and Ulmo (2004)
on the equidistribution properties of Hecke orbits over
the complex numbers, and finally describe recent related
results over the field of p-adic complex numbers. More
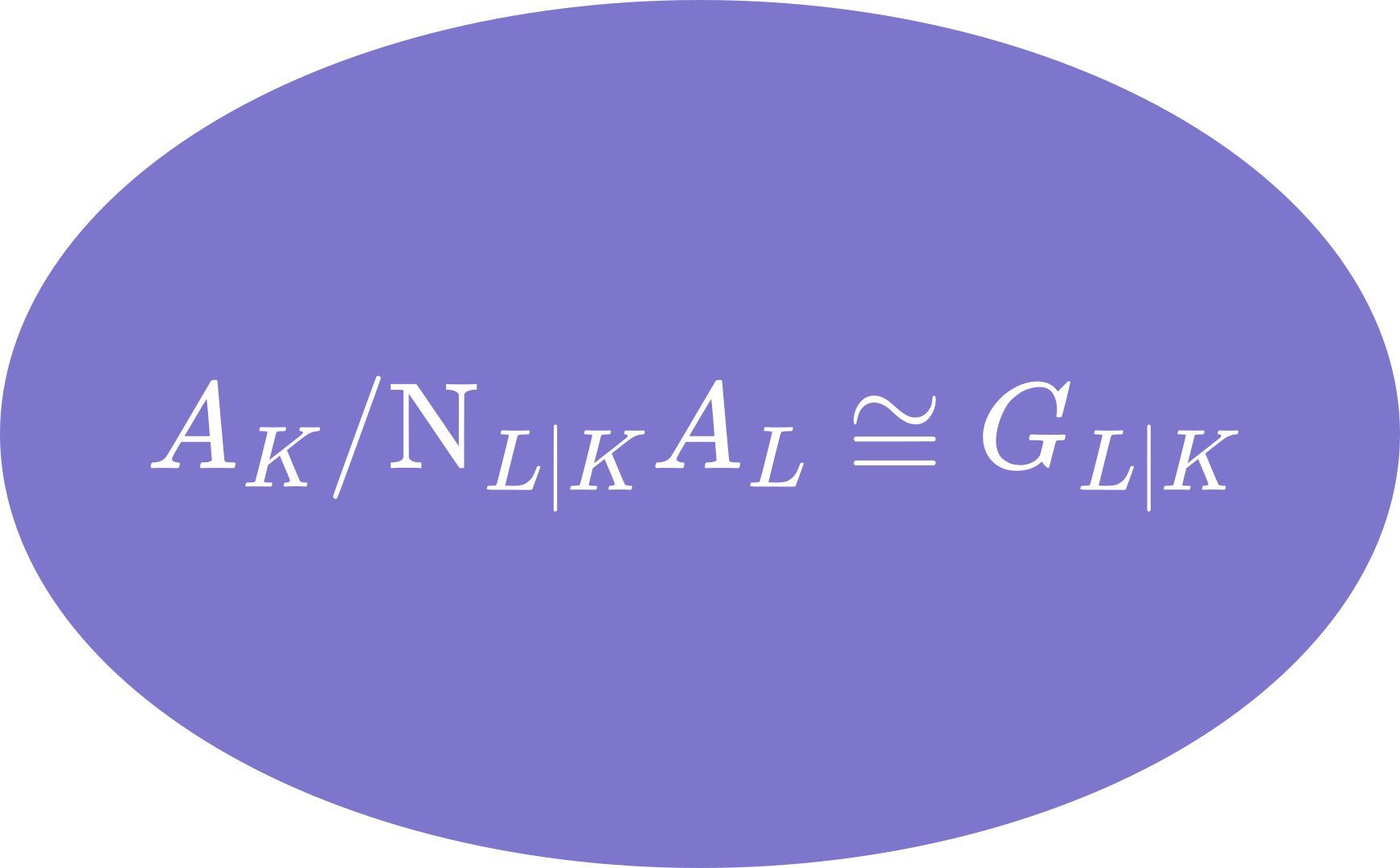
Singular moduli for real quadratic fields
Jan Vonk
In this course, we will explore the work of Gross and Zagier on differences of singular moduli and heights of Heegner points over imaginary quadratic fields, as well as some recent p-adic constructions whose goal is to exhibit similar structures in the more mysterious setting of real quadratic fields. (back)
References
Schedule
| Time | Monday | Time | Tuesday | Wednesday | Thursday | Friday |
|---|---|---|---|---|---|---|
| 09:30-10:00 |
Welcome
|
09:30-10:30 | Jan Vonk II | Graham-Grossi II | Jan Von III | Jan Vonk IV |
| 10:00-11:00 | Sebastián Herrero I |
10:30-11:00 | ☕🍪
|
☕🍪
|
☕🍪
|
☕🍪
|
| 11:00-11:30 |
☕🍪
|
11:00-12:00 | Juan Rodriguez I | Juan Rodriguez II | Juan Rodriguez III | Juan Rodriguez IV |
| 11:30-12:30 | Jan Vonk I | 12:00-14:00 | Lunch | Typical Chilean Barbecue | Lunch | Lunch |
| 12:30-14:30 | Lunch
|
14:00-15:00 | Sebastián Herrero II | Typical Chilean Barbecue | Sebastián Herrero III | Sebastián Herrero IV |
| 14:30-15:30 | Graham-Grossi I | 15:00-15:30 | ☕🍪
|
- | ☕🍪
|
☕🍪 |
| 15:30-16:00 | ☕🍪
|
15:30-16:30 | Graham-Grossi II | - | Graham-Grossi IV | - |




